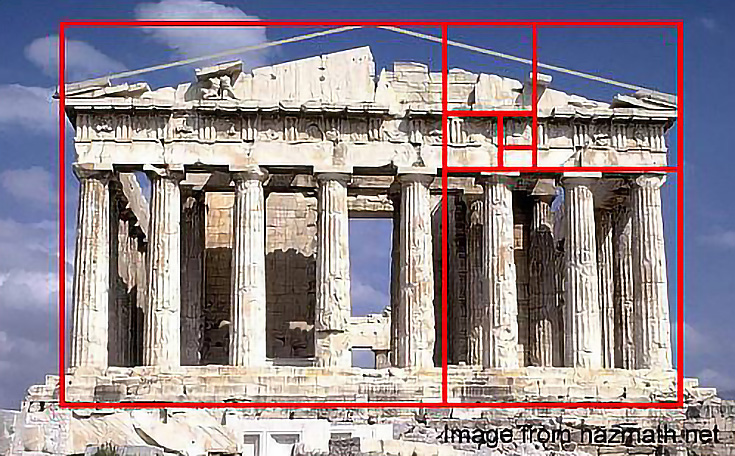
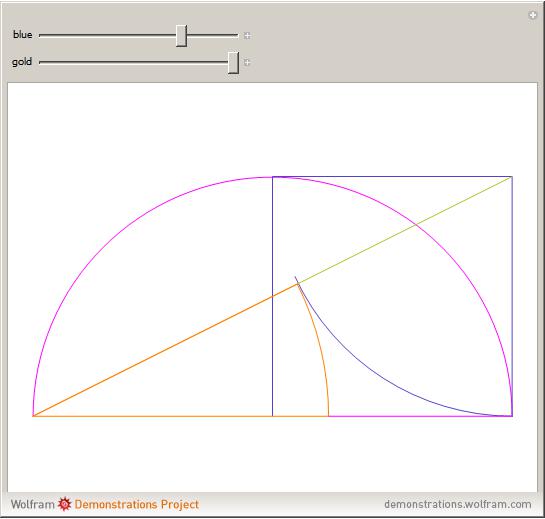
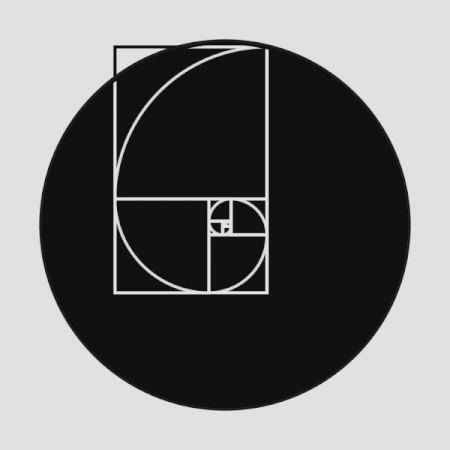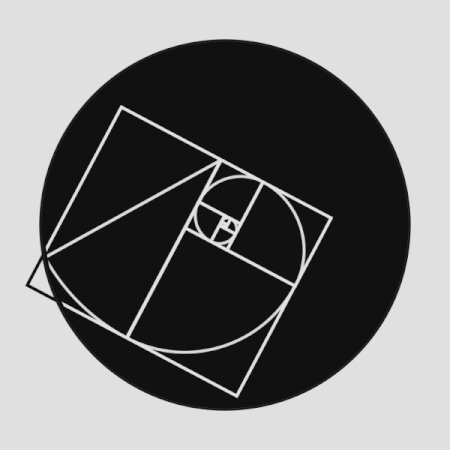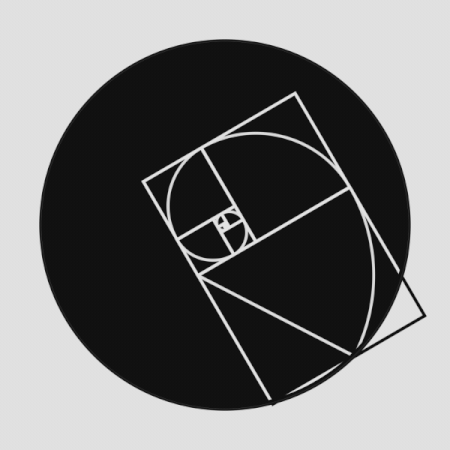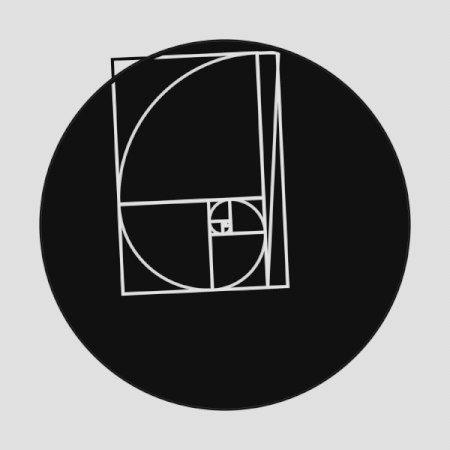
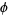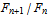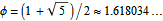Την πιο παλιά και πιο περίπλοκη ιστορία την έχει η χρυσή τομή. Στα μαθηματικά η χρυσή τομή είναι η διαίρεση μιας ευθείας (ενός ευθύγραμμου τμήματος) σε δύο μέρη κατά τρόπο ώστε ο λόγος όλης της ευθείας προς το μεγαλύτερο μέρος να είναι ίσος προς τον λόγο του μεγαλύτερου μέρους προς το μικρότερο.
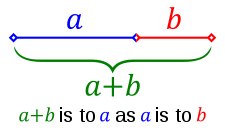
Θυμόμαστε από το σχολείο ότι αυτός ο λόγος θεωρείται ότι εκφράζει την αισθητικά τέλεια αναλογία. Στα αγγλικά έχει πολλές ονομασίες, αλλά οι πιο συνηθισμένες είναι golden section και golden ratio (χρυσός λόγος). Βλ. http://en.wikipedia.org/wiki/Golden_ratio
Στον Ευκλείδη ο όρος ήταν «άκρος και μέσος λόγος»:
Ἄκρον καὶ μέσον λόγον εὐθεῖα τετμῆσθαι λέγεται, ὅταν ᾖ ὡς ἡ ὅλη πρὸς τὸ μεῖζον τμῆμα, οὕτως τὸ μεῖζον πρὸς τὸ ἔλαττον. (Αγγλική μετάφραση στη μεθεπόμενη παράγραφο.)
Στη Wikipedia:
The division of a line into "extreme and mean ratio" (the golden section) is important in the geometry of regular pentagrams and pentagons. The Greeks usually attributed discovery of this concept to Pythagoras or his followers. The regular pentagram, which has a regular pentagon inscribed within it, was the Pythagoreans' symbol.
Euclid's Elements (Στοιχεῖα) provides the first known written definition of what is now called the golden ratio: "A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less."
Από το ίδιο άρθρο:
Luca Pacioli (1445–1517) defines the golden ratio as the “divine proportion” [θεία αναλογία] in his Divina Proportione.
Martin Ohm (1792–1872) is believed to be the first to use the term goldener Schnitt (golden section, χρυσή τομή) to describe this ratio, in 1835.
Since the twentieth century, the golden ratio has been represented by the Greek letter Φ or φ (phi, after Phidias, a sculptor who is said to have employed it) or less commonly by τ (tau, the first letter of the ancient Greek root τομή — meaning cut).
Στο OED:
golden section, (the proportion resulting from) the division of a straight line into two parts so that the ratio of the whole to the larger part is the same as the ratio of the larger part to the smaller, viz. ½(√5 + 1), or 1.61803…; ‘extreme and mean ratio’. This celebrated proportion has been known since the 4th century B.C., and occurs in Euclid (ii. 11, vi. 30). Of the several names it has received, golden section (or its equivalent in other languages) is now the usual one, but it seems not to have been used before the 19th century. (Στο OED δεν υπάρχει το golden ratio.)
O αριθμός φ (phi) είναι γνωστός σαν «χρυσός λόγος» ή «αριθμός του Φειδία» επειδή ο γλύπτης της αρχαιότητας χρησιμοποίησε αυτή την αναλογία στα έργα του.
Από τη χρυσή αναλογία έχουμε επίσης το χρυσό τρίγωνο (golden triangle) και το χρυσό ορθογώνιο (golden rectangle).
Σαν να μην έφταναν τόσα «χρυσά», κάποιοι χρησιμοποιούν και τον χρυσό κανόνα αντί για τη χρυσή αναλογία. Πάντως, σύμφωνα με τα λεξικά, εκτός από την οικονομική σημασία (όπου ο χρυσός κανόνας ή κανόνας χρυσού είναι νομισματικό σύστημα στο οποίο χρησιμοποιείται ο χρυσός ως βάση για τον προσδιορισμό τής νομισματικής αξίας — μεταφράζει το gold standard), η μεταφορική σημασία του χρυσού κανόνα (golden rule) είναι ο κανόνας για να πετύχεις κάτι, ο βασικός κανόνας που πρέπει απαραίτητα να ακολουθήσεις. (π.χ. The golden rule of cooking is to use fresh ingredients.)
Στα αγγλικά golden rule μπορεί να είναι στην αριθμητική η μέθοδος των τριών:
rule of three, a method of finding a fourth number from three given numbers, of which the first is in the same proportion to the second as the third is to the unknown fourth. Also called the golden rule, rule of proportion.
Στην ηθική ο golden rule είναι η αρχή του αλληλοσεβασμού, βασισμένη σε εκείνο που λέει ο Ματθαίος (ζ’ 12) «Πάντα οὖν ὅσα ἐὰν θέλητε ἵνα ποιῶσιν ὑμῖν οἱ ἄνθρωποι, οὕτως καὶ ὑμεῖς ποιεῖτε αὐτοῖς· οὗτος γάρ ἐστιν ὁ νόμος καὶ οἱ προφῆται» (Do unto others as you would be done by). Να φέρεσαι στους άλλους όπως θα ήθελες να σου φέρονται ή, αρνητικά, μην κάνεις στους άλλους ότι δεν θα ήθελες να κάνουν σε σένα. Βλ. http://en.wikipedia.org/wiki/Golden_rule
Για τη χρυσή μετριότητα, στην ιταλική σελίδα της Wikipedia (http://it.wikipedia.org/wiki/Aurea_mediocritas) βρίσκουμε την περιγραφή που θα μπορούσαμε να κάνουμε και στα ελληνικά: το aurea mediocritas στις Ωδές του Οράτιου είναι το «μέτρον άριστον» των αρχαίων Ελλήνων, ο μέσος όρος («ὁμολογεῑται τὸ μέτριον ἄριστον καὶ τὸ μέσον», Αριστοτέλης· «αἱ γὰρ μετριότητες μᾱλλον ἐν ταῑς ἐνδείαις ἢ ταῑς ὑπερβολές ἔνεισιν», Ισοκράτης), η αποφυγή της υπερβολής («μηδέν άγαν»). Αντιστοιχεί στο αγγλικό golden mean ή happy medium, που θα τα μεταφράζαμε: η χρυσή τομή, η μέση λύση, η μέση οδός.
Σήμερα ωστόσο, όπως γράφει και στο ΛΝΕΓ, χρυσή μετριότητα είναι κάποιος που ακολουθεί τον μέσο όρο και δεν έχει κανένα σοβαρό ελάττωμα ούτε όμως και χάρισμα, με αποτέλεσμα να μην προκαλεί το ενδιαφέρον. Μια καλή μετάφραση θα ήταν an overrated mediocrity.
Σταματώ εδώ, να κάνω και μια ρεζουμέ, γιατί είναι μεγάλο το μπέρδεμα:
Από τα ελληνικά στα αγγλικά:
χρυσή τομή = (μαθημ.) golden section | (μτφ.) golden mean, happy medium
χρυσός λόγος, χρυσή αναλογία = golden ratio, golden proportion
άκρος και μέσος λόγος (Ευκλείδη) = extreme and mean ratio
χρυσός κανόνας = (οικον.) (κανόνας χρυσού) gold standard | golden rule
χρυσή μετριότητα = overrated mediocrity
Από τα αγγλικά στα ελληνικά:
golden section = χρυσή τομή
golden ratio, golden proportion = χρυσός λόγος, χρυσή αναλογία
divine proportion = θεία αναλογία
golden mean = (γεωμ., τέχνες) χρυσή τομή | (μτφ.) χρυσή τομή, μέση λύση, μέση οδός
golden rule = χρυσός κανόνας | μέθοδος των τριών
gold standard = κανόνας χρυσού, χρυσός κανόνας

Θυμόμαστε από το σχολείο ότι αυτός ο λόγος θεωρείται ότι εκφράζει την αισθητικά τέλεια αναλογία. Στα αγγλικά έχει πολλές ονομασίες, αλλά οι πιο συνηθισμένες είναι golden section και golden ratio (χρυσός λόγος). Βλ. http://en.wikipedia.org/wiki/Golden_ratio
Στον Ευκλείδη ο όρος ήταν «άκρος και μέσος λόγος»:
Ἄκρον καὶ μέσον λόγον εὐθεῖα τετμῆσθαι λέγεται, ὅταν ᾖ ὡς ἡ ὅλη πρὸς τὸ μεῖζον τμῆμα, οὕτως τὸ μεῖζον πρὸς τὸ ἔλαττον. (Αγγλική μετάφραση στη μεθεπόμενη παράγραφο.)
Στη Wikipedia:
The division of a line into "extreme and mean ratio" (the golden section) is important in the geometry of regular pentagrams and pentagons. The Greeks usually attributed discovery of this concept to Pythagoras or his followers. The regular pentagram, which has a regular pentagon inscribed within it, was the Pythagoreans' symbol.
Euclid's Elements (Στοιχεῖα) provides the first known written definition of what is now called the golden ratio: "A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less."
Από το ίδιο άρθρο:
Luca Pacioli (1445–1517) defines the golden ratio as the “divine proportion” [θεία αναλογία] in his Divina Proportione.
Martin Ohm (1792–1872) is believed to be the first to use the term goldener Schnitt (golden section, χρυσή τομή) to describe this ratio, in 1835.
Since the twentieth century, the golden ratio has been represented by the Greek letter Φ or φ (phi, after Phidias, a sculptor who is said to have employed it) or less commonly by τ (tau, the first letter of the ancient Greek root τομή — meaning cut).
Στο OED:
golden section, (the proportion resulting from) the division of a straight line into two parts so that the ratio of the whole to the larger part is the same as the ratio of the larger part to the smaller, viz. ½(√5 + 1), or 1.61803…; ‘extreme and mean ratio’. This celebrated proportion has been known since the 4th century B.C., and occurs in Euclid (ii. 11, vi. 30). Of the several names it has received, golden section (or its equivalent in other languages) is now the usual one, but it seems not to have been used before the 19th century. (Στο OED δεν υπάρχει το golden ratio.)
O αριθμός φ (phi) είναι γνωστός σαν «χρυσός λόγος» ή «αριθμός του Φειδία» επειδή ο γλύπτης της αρχαιότητας χρησιμοποίησε αυτή την αναλογία στα έργα του.
Από τη χρυσή αναλογία έχουμε επίσης το χρυσό τρίγωνο (golden triangle) και το χρυσό ορθογώνιο (golden rectangle).
Σαν να μην έφταναν τόσα «χρυσά», κάποιοι χρησιμοποιούν και τον χρυσό κανόνα αντί για τη χρυσή αναλογία. Πάντως, σύμφωνα με τα λεξικά, εκτός από την οικονομική σημασία (όπου ο χρυσός κανόνας ή κανόνας χρυσού είναι νομισματικό σύστημα στο οποίο χρησιμοποιείται ο χρυσός ως βάση για τον προσδιορισμό τής νομισματικής αξίας — μεταφράζει το gold standard), η μεταφορική σημασία του χρυσού κανόνα (golden rule) είναι ο κανόνας για να πετύχεις κάτι, ο βασικός κανόνας που πρέπει απαραίτητα να ακολουθήσεις. (π.χ. The golden rule of cooking is to use fresh ingredients.)
Στα αγγλικά golden rule μπορεί να είναι στην αριθμητική η μέθοδος των τριών:
rule of three, a method of finding a fourth number from three given numbers, of which the first is in the same proportion to the second as the third is to the unknown fourth. Also called the golden rule, rule of proportion.
Στην ηθική ο golden rule είναι η αρχή του αλληλοσεβασμού, βασισμένη σε εκείνο που λέει ο Ματθαίος (ζ’ 12) «Πάντα οὖν ὅσα ἐὰν θέλητε ἵνα ποιῶσιν ὑμῖν οἱ ἄνθρωποι, οὕτως καὶ ὑμεῖς ποιεῖτε αὐτοῖς· οὗτος γάρ ἐστιν ὁ νόμος καὶ οἱ προφῆται» (Do unto others as you would be done by). Να φέρεσαι στους άλλους όπως θα ήθελες να σου φέρονται ή, αρνητικά, μην κάνεις στους άλλους ότι δεν θα ήθελες να κάνουν σε σένα. Βλ. http://en.wikipedia.org/wiki/Golden_rule
Για τη χρυσή μετριότητα, στην ιταλική σελίδα της Wikipedia (http://it.wikipedia.org/wiki/Aurea_mediocritas) βρίσκουμε την περιγραφή που θα μπορούσαμε να κάνουμε και στα ελληνικά: το aurea mediocritas στις Ωδές του Οράτιου είναι το «μέτρον άριστον» των αρχαίων Ελλήνων, ο μέσος όρος («ὁμολογεῑται τὸ μέτριον ἄριστον καὶ τὸ μέσον», Αριστοτέλης· «αἱ γὰρ μετριότητες μᾱλλον ἐν ταῑς ἐνδείαις ἢ ταῑς ὑπερβολές ἔνεισιν», Ισοκράτης), η αποφυγή της υπερβολής («μηδέν άγαν»). Αντιστοιχεί στο αγγλικό golden mean ή happy medium, που θα τα μεταφράζαμε: η χρυσή τομή, η μέση λύση, η μέση οδός.
Σήμερα ωστόσο, όπως γράφει και στο ΛΝΕΓ, χρυσή μετριότητα είναι κάποιος που ακολουθεί τον μέσο όρο και δεν έχει κανένα σοβαρό ελάττωμα ούτε όμως και χάρισμα, με αποτέλεσμα να μην προκαλεί το ενδιαφέρον. Μια καλή μετάφραση θα ήταν an overrated mediocrity.
Σταματώ εδώ, να κάνω και μια ρεζουμέ, γιατί είναι μεγάλο το μπέρδεμα:
Από τα ελληνικά στα αγγλικά:
χρυσή τομή = (μαθημ.) golden section | (μτφ.) golden mean, happy medium
χρυσός λόγος, χρυσή αναλογία = golden ratio, golden proportion
άκρος και μέσος λόγος (Ευκλείδη) = extreme and mean ratio
χρυσός κανόνας = (οικον.) (κανόνας χρυσού) gold standard | golden rule
χρυσή μετριότητα = overrated mediocrity
Από τα αγγλικά στα ελληνικά:
golden section = χρυσή τομή
golden ratio, golden proportion = χρυσός λόγος, χρυσή αναλογία
divine proportion = θεία αναλογία
golden mean = (γεωμ., τέχνες) χρυσή τομή | (μτφ.) χρυσή τομή, μέση λύση, μέση οδός
golden rule = χρυσός κανόνας | μέθοδος των τριών
gold standard = κανόνας χρυσού, χρυσός κανόνας